Côte et rareté des cartes
Un peu d'arithmétique pour essayer de comprendre les choses
Nombreux sont les joueurs et/ou collectionneurs de cartes qui se posent des questions sur la côte des cartes. Certes, toutes les cartes n'ont pas la même rareté, mais cela justifie-t-il les écarts de prix constatés ?
En fait, il ne faut pas confondre côte et rareté. La côte est la résultante de deux phénomènes :
- le prix de vente des paquets (starters et boosters) et la rareté des différentes cartes à l'intérieur de chaque type de packaging,
- et la loi de l'offre et de la demande, qui fait que certaines cartes sont plus courues que d'autres.
L'objectif de cet article est de donner des éléments de réponse objectifs sur la première composante, qui dépend totalement de l'approche marketing de l'éditeur. Nous parlerons donc ici de rareté, et de valeur théorique des différentes catégories de rareté, mais pas de côte.
La seconde composante, elle, est totalement subjective, voire parfois totalement irrationnelle comme tous les phénomènes de mode. Mais connaissant la composante objective, vous serez mieux à même d'évaluer la part de la composante subjective dans le prix que l'on vous demande pour telle ou telle carte, et donc de juger s'il est justifié, à vos yeux, en fonction de l'intérêt que vous portez à cette carte ou non.
Prenons un exemple : un starter de Magic 5ème édition V.F. Il comprend 60 cartes et est usuellement vendu 59 F. Si toutes les cartes étaient de rareté identique, chaque carte aurait une valeur intrinsèque de 59 F / 60 cartes = 0,98 F (et des poussières) par carte. Jusque là je pense que vous me suivez
Mais toutes les cartes n'ont pas la même rareté, il nous faut donc corriger cette valeur moyenne pour tenir compte de la distribution réelle des cartes, sur la base des différentes catégories de rareté (vous savez : C pour communes, U pour inhabituelles, R pour rares...), telles qu'elles nous sont indiquées par l'éditeur. Pour chaque catégorie de rareté nous allons donc calculer un « coefficient de rareté », coefficient multiplicatif qui permettra de corriger cette valeur moyenne de 0,98 F. Pour une carte commune, ce coefficient de rareté sera inférieur à 1, et donc la valeur de la carte sera elle-même inférieure à 0,98 F, et inversement, pour une carte rare ce coefficient sera supérieur à 1, voire très supérieur. Ce coefficient doit en outre être tel que la somme des valeurs des cartes composant le paquet reste égale à 59 F (nous ne cherchons pas à faire des bénéfices, juste à identifier la part que chaque carte prend dans le prix du paquet).
À la recherche du coefficient de rareté
Le coefficient de rareté que nous nous proposons de calculer comprendra deux facteurs, correspondant respectivement à :
- la taille (le nombre de cartes possibles) de la catégorie de rareté, ramenée au nombre total de cartes possibles de façon à en faire un pourcentage (ligne A du tableau 1) : le coefficient de rareté est directement proportionnel à A (plus le nombre de cartes possible dans une catégorie de rareté donnée est grand, plus la chance de tomber sur une carte donnée est faible) ;
- la composition du paquet, en considérant le nombre de cartes de chaque catégorie de rareté présentes dans le paquet, ramené au nombre de cartes total dans le paquet. (ligne B du tableau 1) : le coefficient de rareté recherché est inversement proportionnel à B (plus il y a de cartes d'une catégorie de rareté donnée dans le paquet, plus la chance de tomber sur une carte donnée de cette catégorie est élevée).
Le coefficient de rareté recherché est donc proportionnel à A x 1/B = A/B. Et comme A et B sont tous deux des pourcentages, A/B possède la propriété recherchée, à savoir conserver la valeur totale du paquet (je vous laisse la démonstration à titre d'exercice). Ce qui signifie que nous pouvons prendre A/B comme coefficient de rareté sans normalisation supplémentaire. Il ne nous reste plus qu'à multiplier la valeur moyenne de 0,98 F par carte par ce coefficient pour obtenir, pour chaque catégorie de rareté, la valeur d'une carte appartenant à cette catégorie (voir tableau ci-après). Ou plutôt que la valeur, disons la part du prix du paquet que représente chacune des cartes qui le compose.

Valeurs théoriques des cartes d'un starter Magic 5ème édition V.F.
Vérification : 22 terrains à 0,12 F + 26 cartes communes à 0,83 F + 9 cartes inhabituelles à 1,93 F + 3 cartes rares à 5,78 F = 58,93 F. Le compte est bon (aux erreurs d'arrondis sur les centimes près - si vous faites les calculs avec suffisamment de décimales, ça tombe juste, croyez-moi ou vérifiez-le avec votre tableur favori).
Et les boosters, alors ?
Le calcul précédent serait valable dans un monde où il n'y aurait que des starters. Le problème c'est qu'il y a aussi des boosters ! Et qu'en plus, les génies du marketing de Wizards of the Coast ont décidé que les boosters ne contiendraient pas de terrains de base (catégorie de rareté T).
Refaisons donc les calculs précédents en considérant la distribution des cartes d'un booster, et en ignorant la catégorie T (de façon à conserver des pourcentages). Le résultat est donné par le tableau ci-dessous.
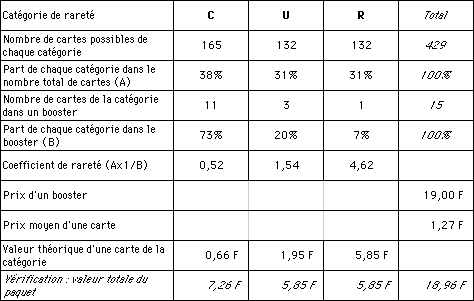
Valeurs théoriques des cartes d'un booster Magic 5ème édition V.F.
Que constatons-nous ? Les valeurs théoriques calculées pour les catégories U et R sont identiques à moins de 10 centimes près. Ils sont forts chez WotC ! Pour les cartes communes, la fourchette est un peu plus large : entre 0,66 F et 0,83 F. Mais c'est néanmoins une bonne indication.
Et la côte dans tout ça ?
En gros, cela signifie que lorsque la côte pour une carte rare de la 5ème édition est, par exemple, de 10 F, il y a déjà plus de 4 F de surcôte par rapport à la valeur théorique déduite de la rareté réelle de la carte... Surcôte justifiée si la carte est d'un intérêt particulier mais n'oubliez pas que la côte n'est là que pour donner un point de départ à la transaction. Une bonne négociation, c'est une négociation dont chacun sort content !
Et les autres éditions ?
Bien sûr, ce calcul peut se faire pour toutes les éditions et extensions de Magic, de façon absolument identiques pour celles qui présentent des catégories de rareté simples (nous l'avons fait pour vous, vous trouverez un tableau récapitulant tous les résultats à la fin de l'article), et d'une façon un peu plus compliquée pour celles qui ont des U3 ou des R6... sur lesquelles nous allons nous pencher tout de suite !
Les cas particuliers
Seules trois extensions ne se limitent pas à des catégories de rareté simple : Renaissance, Terres Natales et Alliances.
Renaissance
De point de vue de la composition des boosters l'extension Renaissance ne comporte que 2 catégories de rareté : C et U. Un booster de 8 cartes est composé de 6 C et de 2 U, et est (était) vendu 12 F. Mais quand on y regarde de plus près, les problèmes surgissent, chacune de ces deux catégories recouvrant en fait plusieurs sous-catégories de cartes, qui n'ont pas la même fréquence d'apparition sur les planches (de 121 cartes) qui servent à imprimer les différentes catégories de rareté.
Ainsi la planche C comporte 121 cartes se décomposant en :
- 14 cartes C1 n'apparaissant qu'une fois sur la planche,
- 7 cartes C2 qui y apparaissent 2 fois,
- 31 cartes C3 qui y apparaissent 3 fois.
Une simple « règle de 3 » permet donc de dire que sur les 6 cartes C d'un booster, il y a en moyenne :
- 6 x ( 14 / 121 ) = 0,69 carte C1,
- 6 x ( 2 x 7 / 121 ) = 0,69 cartes C2,
- 6 x ( 3 x 31 / 121 ) = 4,61 cartes C3,
ce qui permettra de calculer des coefficient B différents pour les catégories C1, C2 et C3.
De même, les 121 cartes de la planche U se décomposent en :
- 49 cartes U1 n'apparaissant qu'une fois sur la planche,
- 2 cartes U2 apparaissant 2 fois chacune,
- 14 cartes U3 apparaissant 3 fois chacune,
- 2 cartes U4 apparaissant 4 fois chacune,
- 3 cartes U6 apparaissant 6 fois chacune.
La même miraculeuse règle de 3 permettra de calculer le nombre moyen de cartes U1, U2, U3, U4 et U6 dans un booster :
- 2 x ( 49 / 121 ) = 0,81 carte U1,
- 2 x ( 2 x 2 / 121 ) = 0,07 carte U2,
- 2 x ( 3 x 14 / 121 ) = 0,69 carte U3,
- 2 x ( 4 x 2 / 121 ) = 0,13 carte U4,
- 2 x ( 6 x 3 / 121 ) = 0,30 carte U6.
Nous avons alors tous les éléments pour faire le calcul, et le tableau suivant donne les résultats.
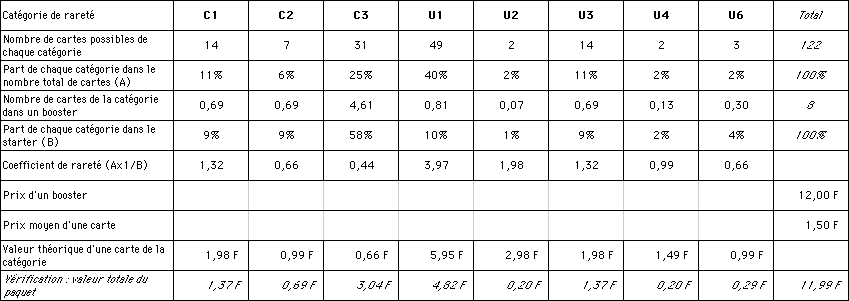
Valeurs théoriques des cartes Renaissance
Il est amusant de noter que, malgré leur qualificatif respectif de "commune" et de "inhabituelle", une U3 a exactement la même rareté qu'une C1, et une U6 qu'une C2, et que les U4 et U6 sont moins rares qu'une C1 !
Terres Natales
Comme l'extension Renaissance, l'extension Terres Natales ne comporte que 2 catégories de rareté (C et U) avec des boosters de 8 cartes composés de 6 C et de 2 U, et vendu 12 F. Mais là en plus, on a jugé intéressant (?) de sortir plusieurs fois la même carte avec des illustrations différentes...
Ainsi la planche C comporte 121 cartes se décomposant en 21 cartes C1 n'apparaissant qu'une fois, et 25 cartes C2 qui y apparaissent 4 fois, avec deux dessins différents (2 fois chacun des dessins). La règle de 3 précédente permet donc de dire que sur les 6 cartes C d'un booster, il y a en moyenne :
- 6 x ( 21 / 121 ) = 1,04 carte C1,
- 6 x ( 25 x 2 x 2 / 121 ) = 4,96 cartes C2,
ce qui permettra de calculer des coefficient B différents pour les catégories C1 et C2. Notons au passage que pour le calcul du coefficient A, la catégorie C2 comptera pour 50 cartes, puisque chacune des 25 cartes existe en deux versions.
De même, les 121 cartes de la planche U se décomposent en 43 cartes U1 n'apparaissant qu'une fois et 26 cartes U3 y apparaissant 3 fois chacune (avec le même dessin). La règle de 3 permettra de calculer le nombre moyen de cartes U1 et U3 dans un booster :
- 2 x ( 43 / 121 ) = 0,71 carte U1;
- 2 x ( 26 x 3 / 121 ) = 1,29 carte U3.
Nous avons alors tous les éléments pour faire le calcul, et le tableau ci-dessous donne les résultats.
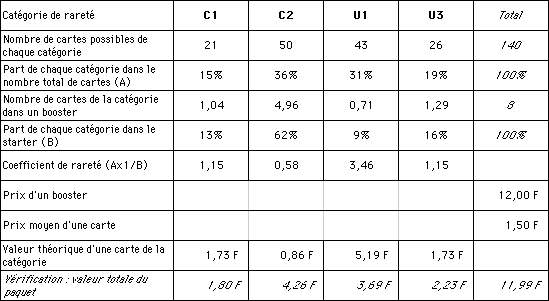
Valeurs théoriques des cartes Terres Natales
Là aussi on constate qu'une U3 a exactement la même rareté qu'une C1.
Alliances
On atteint là le summum de la complexité ! Trois catégories (C, U et R) sont utilisées, chacune subdivisées en 2 sous-catégories sur des planches de 110 cartes :
- C1 : 40 cartes existant en 2 dessins différents chacun une fois sur la planche C,
- C2 : 10 cartes existant en 2 dessins différents, présents l'un 1 fois et l'autre 2 fois sur la planche C ; en termes de rareté, il nous faut donc distinguer le dessin qui n'apparaît qu'une fois de celui qui apparaît deux fois : ils sont appelés C21 et C22 dans le tableau des résultats,
- U2 : 40 cartes présentes 2 fois sur la planche U, avec le même dessin,
- U3 : 5 cartes existant en 2 dessins différents, présents chacun 3 fois sur la planche U,
- R2 : 46 cartes présentes 2 fois sur la planche R, avec le même dessin,
- R6 : 3 cartes présentes 6 fois sur la planche R, avec le même dessin,
Et en plus, la composition des boosters, de 15 cartes et vendus 16 F, ne s'exprime pas en nombre entiers... [Si vous connaissez la règle exacte je suis preneur] Sur 15 cartes, on trouve toujours 10 cartes C, mais le nombre de cartes U varie entre 3 et 4, et celui des cartes R entre 1 et 2. Une statistique effectuée sur un display de 36 boosters montre qu'en moyenne on obtient 3,75 cartes U et 1,25 carte R, c'est à dire que dans un booster sur 4 une carte U est remplacée par une carte R. Heureusement que nous utilisons un tableur pour prendre tous ces paramètres en compte !
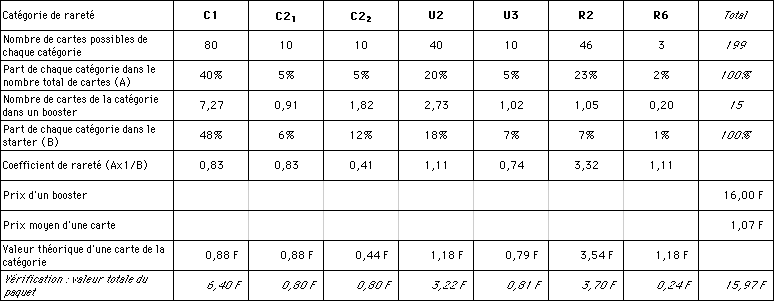
Valeurs théoriques des cartes Alliances V.F.
Là aussi, remarquons qu'une R6 est équivalente à une U2, et qu'une C1 (ou C21) est plus rare qu'une U3.
En résumé
Si vous ne devez retenir qu'une chose, le tableau ci-après récapitule les valeurs théoriques des différentes catégories de rareté de toutes les éditions et extensions de Magic (à l'exception de l'Édition Originale Française pour laquelle je ne dispose pas des données de distribution, et des starters préconstruits qui sont encore des cas particuliers... très particuliers !) :

Récapitulatif des valeurs théoriques des différentes éditions et extensions de Magic
Si l'on regroupe ces résultats en fourchettes de 5 centimes (on prenant des valeurs moyennes pour les extensions existant à la fois en starters et en boosters), on obtient le tableau récapitulatif suivant :
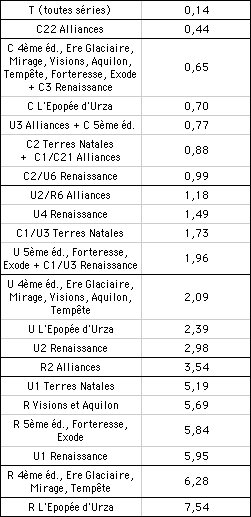
Récapitulatif des valeurs théoriques des différentes éditions et extensions de Magic
Regroupement par fourchettes de 5 centimes
A noter que les calculs ont été faits sur la base des prix de vente des starters et boosters au moment de la sortie de l'extension. L'augmentation de prix de 1998 n'a été appliquée qu'à partir de l'Héritage d'Urza, alors qu'en pratique elle a eu un effet rétroactif sur toutes les séries encore en vente à cette époque.
Et maintenant ?
Et maintenant, vous avez tous les éléments pour regarder la côte avec un peu de recul. Bien sûr, ces chiffres doivent être réévalués pour tenir compte de la raréfaction croissante des séries les plus anciennes, de l'intérêt pour le jeu de telle ou telle carte... Mais vous avez les éléments de base pour juger objectivement de la réalité. Et puis, si vous ne faites pas du commerce mais êtes plutôt un adepte de l'échange - ce qui me semble de loin préférable - vous pouvez utiliser les valeurs théoriques ainsi calculées comme base d'échange sans vous casser la tête. Les échanges, ça fait partie intégrante du plaisir de Magic !
Mieux encore, vous êtes désormais à même de faire les calculs pour les nouvelles extensions à venir, ou pour d'autres jeux. Et quand il n'existe pas de côte publiée, c'est la seule façon de se faire une idée objective de la valeur respective des différentes cartes avant de se lancer tête baissée dans une transaction hasardeuse. [Mais si vous préférez ne pas faire les calculs par vous-mêmes, n'hésitez pas à demander ! Il est tout à fait possible d'envisager à l'avenir d'autres articles consacrés à d'autres jeux. D'autant plus que chaque éditeur a généralement tenu à ajouter son grain de sel en complexifiant le système initialement conçu par Wizards of the Coast.]
Mais surtout, n'oubliez pas, il s'agit de jeu et de collection ici, c'est à dire de plaisir et de passion. Ne laissez pas les questions d'argent vous gâcher la vie !
Postface pour le site Web
Mais, me direz-vous, les tarifs pratiqués sur ce site ne sont pas exactement les mêmes que les valeurs que l'on calcule dans cet article ? C'est exact, et en voilà l'explication.
- Les valeurs théoriques utilisées pour les échanges sont exactement calculées selon le principe expliqué dans cet article, mais la base statistique utilisée est tout simplement l'état courant de ma propre collection, qui évolue au fur et à mesure des mes échanges / achats / ventes. Ce qui signifie que les catégories de rareté les plus demandées deviennent plus rares, et donc ont une valeur théorique d'échange plus élevée... Logique, non ?
- Les prix de vente des cartes sont calculées exactement selon le même principe, mais en prenant cette fois pour échantillon statistique l'ensemble des cartes à vendre et non l'ensemble des cartes possédées. Là aussi, c'est logique. Ensuite j'applique un minimum de 0,10 € par carte (pour tenir compte du temps passé à la chercher, mettre à jour le fichier, etc.), et des réductions significatives pour la vente par lots (10% pour un lot de 10 cartes de même rareté sans aucun tri préalable, et donc pouvant éventuellement contenir des doubles, 20% pour un lot de 50, 40% pour un lot de 100, et 50% pour les lots "super-promo"). Et si c'est beaucoup moins cher que ce que vous pouvez trouver ailleurs, tant mieux pour vous ! Quant à moi, il ne me sert à rien d'accumuler des doubles pour des échanges qui ne se feront jamais...